高斯光束传播

This is Section 5.1 of the Laser Optics Resource Guide.

许多激光光学应用都假设激光束是高斯光束，其辐照度分布符合理想高斯分布。其实，所有实际的激光束都会与理想高斯行为有一些偏差。M²因子（也称为光束质量因子）比较真实激光束和衍射极限高斯光束的性能。¹ 高斯辐照度分布以光束中心为轴对称，并且随着光束中心与传播方向垂直距离的增加而减小（图 1）。该分布由公式 1² 描述：

(1)$$ I \! \left( r \right) = I_0 \exp{\left( \frac{-2 r^2}{w \! \left( z \right)^2} \right)} = \frac{2P}{\pi w \! \left( z \right)^2} \exp{\left( \frac{-2 r^2}{w \! \left( z \right)^2} \right)} $$

在等式 1中，I₀ 为光束中心处的峰值辐照度，r 为离轴的径向距离，w(z) 为激光束的半径，辐照度为 I₀ 的 1/e² (13.5%)，z 为波前为平面时从平面传播的距离，P 为光束的总功率。

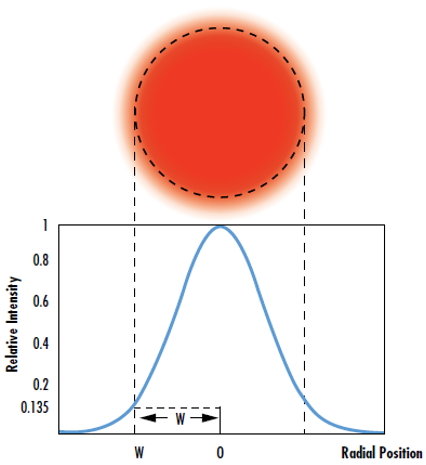
图 1: 高斯光束的束腰定义为辐照度为其最大值 1/e<sup>2</sup> (13.5%)的位置

图 1: 高斯光束的束腰定义为辐照度为其最大值 1/e² (13.5%) 的位置

不过，当光束在空间中传播时，这种辐照度剖面并不保持恒定，因此w(z) 依赖于z。由于衍射作用，高斯光束会从束腰 (w₀) 区域收敛并发散，而束腰 (w₀) 区域是光束直径达到最小值的地方。光束收敛和发散都在束腰两端发散角 θ 范围内（图 2）。束腰和发散角均从坐标轴上测量，其关系如公式 2 和公式 3 所示²：

(2)$$ w_0 = \frac{\lambda}{\pi \theta} $$

(3)$$\theta = \frac{\lambda}{\pi w_0} $$

在上面的等式中，λ 是激光的波长，θ 是远场近似值。因此，θ 不能准确反映束腰附近的发散，但与束腰的距离越远，它便更准确。由公式 3 可知，束腰越小，发散角越大；束腰越大，发散角越小（或者光束越直）。这就解释了为什么激光扩束镜可以通过增加光束直径来减小光束发散。

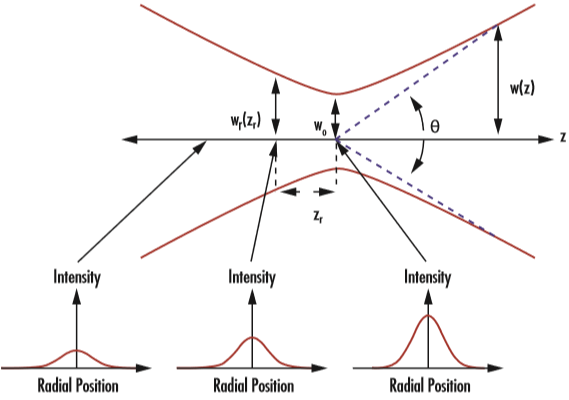
图 2: 高斯光束通过其束腰 (w₀)、瑞利长度 (z_R) 和发散角 (θ) 定义

束腰区域光束直径的变化定义为:

(4)$$ w \! \left( z \right) ^2 = w^2 _0 + \theta ^2 z^2 = w^2 _0 + \left( \frac{\lambda}{\pi w_0 ^2} \right)^2 z^2 $$

(5)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} $$

高斯光束的瑞利长度定义为 z 值，此长度是光束横截面积为束腰两倍的位置。w(z) 增加至 √2w₀. 时会发生这种情况。利用公式 5，瑞利长度 (z_R) 可以表示为

(6)$$ z_R = \frac{\pi w_0 ^2}{\lambda } $$

这使得 w(z) 也与 z_R 相关:

(7)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} = w_0 \sqrt{1 + \left( \frac{z}{z_R} \right)^2} $$

束腰处的激光波前是平面，相对束腰区域的距离增加时，波前会再次成形。这是因为波前曲率半径开始接近无穷大。波前的曲率半径从束腰处的无穷大减小到瑞利长度处的最小值，在远离激光器时重新回到无穷大（图 3）；束腰两端都是如此。³

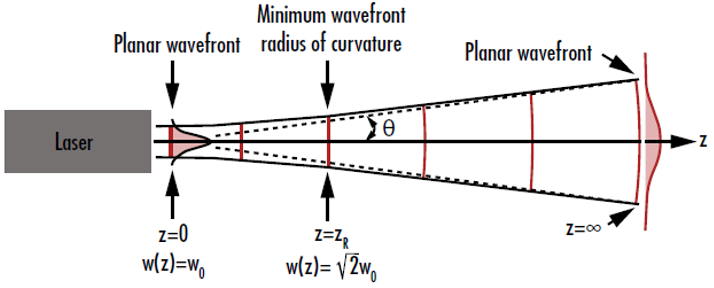
图 3: 当高斯光束离束腰非常近和非常远时，其波前曲率接近于零

高斯光束处理

许多激光光学系统需要处理激光光束，而不是简单地使用“原始”光束。这可以通过使用光学组件（如透镜、反射镜、棱镜等）实现。下面是一些最常见的高斯光束使用指南。

高斯光束的薄透镜公式

理想薄透镜的性能可以采用以下公式描述²:

(8)$$ \frac{1}{s'} = \frac{1}{s} + \frac{1}{f} $$

在 公式 8 中，s’ 是透镜到图像的距离，s 是透镜到物体的距离，f 是透镜的焦距。如果物体和图像在透镜的相对两侧，则 s 为负值，s’ 为正值。该公式忽略了真实透镜的厚度，因此只是实际情况的简单近似（图 4）。薄透镜公式也可以采用无因次形式表示，即公式两边同时乘以 f:

(9)$$ \frac{f}{s'} = \frac{f}{s} + 1 \text{ or } \frac{1}{\left( \frac{s'}{f} \right)} = \frac{1}{\left( \frac{s}{f} \right)} + 1 $$

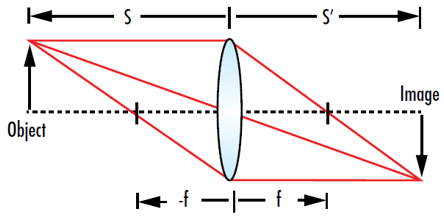
图 4: 薄透镜公式能够在已知透镜到物体的距离 (s) 和透镜的焦距(f) 时确定图像的位置 (s’ )

除了描述成像应用外，薄透镜等式还适用于高斯光束的聚焦，将输入光束的束腰作为物体，输出光束的束腰作为图像。高斯光束经过无像差的理想透镜后，仍然是高斯光束。1983 年，Sidney Self 开发了一种计算高斯传播的薄透镜公式⁴:

(10)$$ \boxed{ \frac{1}{s'} = \frac{1}{ s + \frac{z_R ^2}{\left( s + f \right)}} + \frac{1}{f} } $$

通过将 s 的绝对值与 s’ 相加，计算激光器到聚焦点的总距离。公式 10也可以采用无因次形式表示，即等式两边同时乘以 f:

(11)$$ \frac{f}{s'} = \frac{1}{\left( \frac{s}{f} \right) + \frac{\left( \frac{z_R}{f} \right)^2}{\left( \frac{s}{f} + 1 \right)} } + 1 $$

当 z_R/f 趋于 0 时，这个等式接近标准的薄透镜公式，允许将标准薄透镜公式用于长焦距透镜。通过透镜成像后，可以使用公式 10 和11 找到束腰的位置（图 5）。

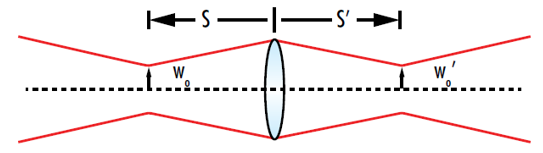
图 5: 高斯光束重聚焦时的“物体”为输入束腰，“图像”为输出束腰

标准化图像距离 (s’/f ) 与标准化物体距离 (s/f ) 的对比图显示给定标准化瑞利长度 (z_R/f) 下可能的输出束腰位置（图 6）。这张图表明通过透镜聚焦的高斯光束与传统的薄透镜成像相比有几个关键的区别。高斯光束成像具有最小和最大的可能成像距离，而传统的薄透镜成像没有。重新聚焦的高斯光束的最大成像距离位于距物体 -(f + z_R) 处，而不是 –f 处。图中 s/f = -1 和 s’/f = 1 的点表示如果输入在凸形透镜的前焦点处，输出束腰将在透镜的后焦点处。

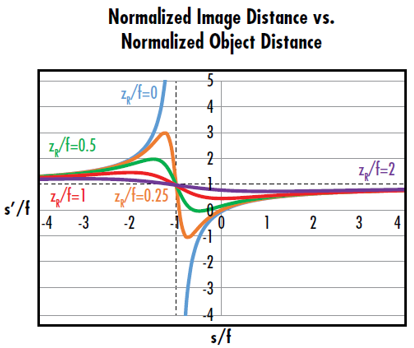
图 6: z<sub>R</sub>/f=0 的曲线对应于传统的薄透镜公式。z<sub>R</sub>/f>0 的曲线表
明，高斯成像具有瑞利长度所定义的最小和最大成像距离

图 6: z_R/f=0 的曲线对应于传统的薄透镜公式。z_R/f>0 的曲线表明，高斯成像具有瑞利长度所定义的最小和最大成像距离

为了理解光束穿过透镜后的束腰和瑞利长度，需要知道系统的放大倍率 (α)，其计算公式为:

(12)$$ \alpha = \frac{w'_0}{w_0} = \frac{1}{\sqrt{1 - \left( \frac{s}{f} \right)^2 + \left( \frac{z_R}{f} \right)^2}} $$

其中 w₀ 为透镜前束腰，w₀’ 为透镜后束腰。然后可以改写高斯光束的薄透镜公式，以包括透镜后光束的瑞利长度 (z_R'):

(13)$$ \boxed{ \frac{1}{ s' + \frac{{z'}_R ^2}{\left( s' - f \right)} } = \frac{1}{s} + \frac{1}{f} } $$

如果透镜在束腰处(s=0)，上述公式将失效。放大倍数常量平方值的倒数可以用来关联束腰的大小和位置³:

(14)$$ \frac{1}{\alpha ^2} = \frac{ \left| s \right| - f}{s' -f} = \left( \frac{w_0}{w'_0} \right)^2 $$

将高斯光束聚焦到一个点上

In many applications, such as laser materials processing or surgery, it is highly important to focus a laser beam down to the smallest spot possible to maximize intensity and minimize the heated area. In cases such as these, the goal is to minimize w₀' (Figure 7). A modified version of Equation 14 may be used to identify how to minimize the output beam waist³:

(15)$$ \frac{\left( \left| s \right| -f \right)^2}{f^2 - \left( \frac{{w'}_0}{\theta} \right)^2 } = \left( \frac{w_{0}}{{w'}_0} \right)^2 $$

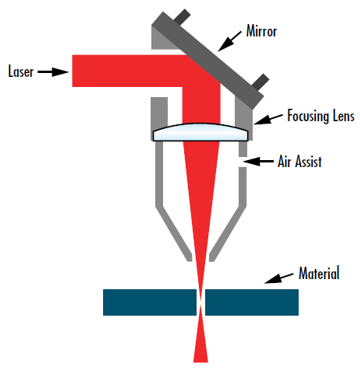
Figure 7: 将激光束聚焦到尽可能小的尺寸对于包括这种激光切割装置在内的广泛应用至关重要

两边同时乘以方程左边的分母，然后再乘以 (w₀')²后，公式 15 变成:

(16)$$ \left( \left| s\right| -f \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - \left( \frac{w_0}{\theta} \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - z_R ^2 $$

(17)$$ \left( w'_0 \right) ^2 \left[ \left( \left| s \right| - f \right)^2 + z_R ^2 \right] = f^2 w_0 ^2 $$

Solving for w₀' results in:

(18)$$ \boxed{ w'_0 = w_0 \frac{f}{\sqrt{\left( \left| s \right| - f \right) ^2 + z_R ^2}} = \alpha w_0 } $$

(19)$$ \boxed{ \alpha = \frac{f}{\sqrt{\left( \left| s \right| -f \right)^2} + z_R ^2} } $$

可以通过减少透镜焦距和 |s|-f 来尽可能缩小聚焦束腰。公式 18 中w₀ 旁边的参数被定义为另一种形式的放大倍率常数 α，用于比较入射光束和经过透镜后的输出光束的值（图 8）.³

(20)$$ \theta ' = \frac{\lambda}{\pi w'_0} = \frac{\lambda}{\pi \alpha w_0} = \frac{\theta}{\alpha} $$

(21)$$ z'_R = \frac{w'_0}{\theta '} = \frac{\alpha w_0}{\left( \frac{\theta}{\alpha} \right)} = \alpha ^2 z_R $$

(22)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right)} $$

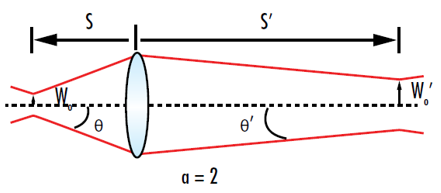
图 8: 对于放大倍率 2，输出束腰将是输入束腰的两倍，输出发散将是输入光束发散的一半

There are two limiting cases which further simplify the calculations of the output beam waist size and location: when s is much less than z_R or much greater than z_R.³ When the lens is well within the laser’s Rayleigh range, then s << z_R and (|s|-f)²<〖z_R〗². Equation 19 simplifies to:

(23)$$ \alpha = \frac{f}{z_R} = \frac{f \theta}{w_0} $$

这也简化了输出光束的束腰、发散度、瑞利长度和束腰位置的计算:

(24)$$ \theta ' = \frac{\theta}{\alpha} = \frac{ \theta w_0}{f \theta} = \frac{w_0}{f} $$

(25)$$ z_R ' = \alpha ^2 z_R = \frac{f^2}{z_R ^2} z_R = \frac{f^2}{z_R} $$

(26)$$ \boxed{ w'_0 = \alpha w_0 = f \theta } $$

(27)$$ \boxed{ s' = f + \alpha^2 \left( \left| s \right| - f \right) = f + \frac{ \left| s \right| f^2}{z_R ^2} \approx f } $$

当 s >> z_R 时，透镜到聚焦点的距离等于透镜的焦距。

另一种限制情况是，透镜距离瑞利长度和 s >> z_R 很远，公式 19 将简化为:

(28)$$ \alpha = \frac{f}{\left| s \right|} $$

这使输出束腰直径等于:

(29)$$ w'_0 = \frac{f w}{ \left| s \right|} $$

与 s << z_R 时相同，输出束腰、发散度、瑞利长度和束腰位置的计算也简化了:

(30)$$ \theta ' = \frac{\theta}{\alpha} = \frac{\left| s \right| \theta }{f} $$

(31)$$ z'_R = \alpha^2 z_R = \frac{f^2 z_R}{s^2} $$

(32)$$ \boxed{ w'_0 = \alpha w_0 = \frac{fw_0}{\left| s \right|} } $$

(33)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right) = f + \frac{\left( \left| s \right| - f \right) f^2}{s^2} = f + \frac{f^2}{ \left| s \right|} \approx f } $$

s >> z_R, 时，从透镜到聚焦点的距离等于透镜的焦距。

这两个结果都具有直观意义，因为在束腰处和离束腰很远的位置，光束的波前都近似平面。在这些位置，光束几乎完全平行（图 9）。根据标准的薄透镜公式，准直输入的成像距离等于透镜的焦距。

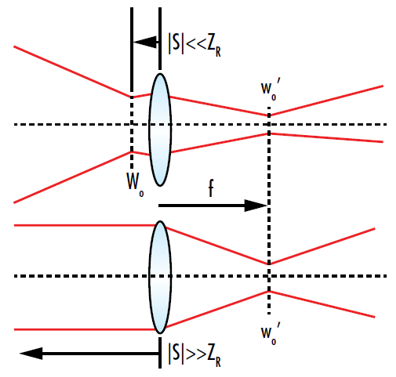
图 9: 如果输入光束束腰离透镜很近或很远，高斯光束经过透镜后，其聚焦位置就会位于透镜的焦点上。这是因为输入光束在这些点上近似平行

高斯焦距变换

Counterintuitively, the intensity of a focused beam in a target at a fixed distance (L) away from the lens is not maximized when the waist is located at the target. The intensity on the target is actually maximized when the waist occurs at a location before the target (Figure 10). This phenomenon is known as Gaussian focal shift.

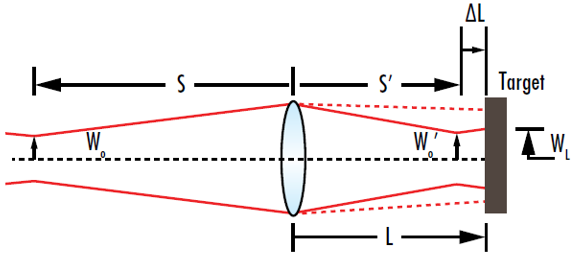
图 10: 目标处的光束半径在聚焦光束的束腰出现在目标前的特定位置，而不是目标处时达到最小值

本文未涵盖详细的推导，但目标的光束半径可以通过以下表达式描述:⁵:

(34)$$ w_L = \frac{w_0}{z_R} \left[ f^2 - 2 \left( \left| s \right| - f \right) \left( L - f \right) + \left( \frac{L-f}{\alpha} \right)^2 \right] $$

区分关于聚焦透镜的焦距 (f) 的公式 34，并求出 ^d⁄_df [w_L (f )]=0 时的 f 可以得到透镜焦距，从而使目标位置的光束半径最小，因而强度最大。

(35)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = \frac{w_0}{z_R} \left[ 2f + 2 \left( \left| s \right| -f \right) + \left( L - f \right) - \frac{2 \left( L - f \right)}{\alpha ^2} \right] $$

(36)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = 0 \text{ when } f = \left( \frac{1}{\left| s \right| + \frac{z_R ^2}{\left| s \right|}} + \frac{1}{L} \right) ^{-1} $$

当|s|趋近于零或无穷大时，f = L 时 ^d⁄_df [w_L (f )]=0。在这两种情况下，输入光束都近似准直光，因此可以得出最小光束半径将出现在透镜的焦点上。

准直高斯光束

在发散度为 0 的情况下无法实现真正的准直光束，但可以通过最小化发散度或最大化观察点与最近束腰之间的距离来实现近似准直光束。由于输出发散度与放大倍率常数 α 成反比，因此输出发散在|s|= f时达到最小值（图 11）。

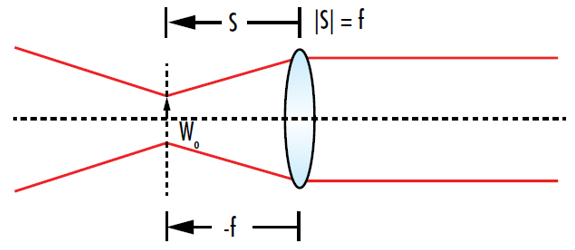
图 11: 要对高斯光束进行准直，束腰到准直透镜的距离应该等于透镜的焦距

参考文献

Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
“Gaussian Beam Optics.” CVI Laser Optics, IDEX Optics & Photonics.
O'Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
Katz, Joseph, and Yajun Li. “Optimum Focusing of Gaussian Laser Beams: Beam Waist Shift in Spot Size Minimization.” Optical Engineering, vol. 33, no. 4, Apr. 1994, pp. 1152–1155., doi:10.1117/12.158232.

上个章节下个章节