光束质量和斯特列尔比

This is Sections 6.2, 6.3, 6.4, and 6.5 of the Laser Optics Resource Guide.

In order to accurately predict the real-world performance and quality of a laser, it is necessary to understand the laser’s M² factor, which describes the quality of the beam. 。一旦了解了激光器的性能，定义与激光器一起使用的任何光学系统的真实性能将有助于了解最终系统的性能。将光学系统的实际性能与其理想性能进行比较，利用斯特列尔比使性能达到衍射极限。

M² 因子

激光的光束质量由 M² 因子表征，将光束的真实形状与理想高斯光束的形状进行比较。ISO 标准 11146 将 M² 因子定义为¹:

(1)$$ M^2 = \frac{\pi w_0 \theta}{\lambda} $$

In Equation 1, w₀ is the beam waist, θ is the divergence angle of the laser, and λ is the lasing wavelength (Figure 1). As defined in our Gaussian Beam Propagation application note, the divergence angle of a Gaussian beam is determined by the following equation:

(2)$$ \theta = \frac{\lambda}{\pi w_0} $$

将找到的发散角代入等式 1 后，高斯光束 M² 因子的等式将简化为：

(3)$$ M^2 = \frac{\pi w_0}{\lambda} \times \frac{\lambda}{\pi w_0} = 1 $$

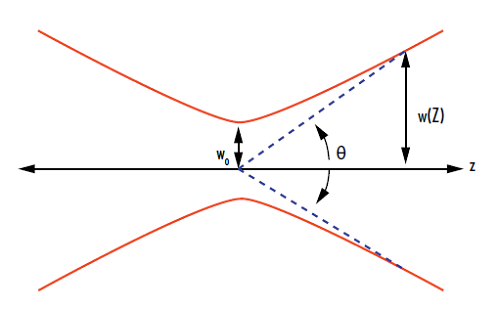
图 1: 激光束发散角和束腰图解

因此，M² 因子为 1 对应于衍射极限高斯光束。M² 因子（大于 1）越大，与理想高斯光束的偏差也越大。无法达到小于 1 的值。厄米高斯模的 M² 因子在 x 轴方向通过 (2n + 1) 得出，在 y 方向通过 (2m + 1) 得出。例如，TEM₁₃的 M² 因子在 x 方向上是 3，在 y 方向上是 ²。典型氦氖激光器的 M² 因子在 1 到 1.1 之间。

Along with a laser beam’s optical power, the M² factor determines the radiance of the beam. The M² factor can also be used to approximate the radius of a beam as it propagates by replacing the wavelength of a laser with the wavelength multiplied by the M² factor found in all of the equations in the Gaussian Beam Propagation application note.³

M² 因子很重要，因为它表示激光束在给定发散度下的聚焦能力。M² 因子越低，激光器的聚焦越精密，光束内功率的利用率越高，潜在有效功率越高。

测量 M² 并不像在激光轴单一平面上测量光束轮廓那么简单。ISO11146 规定，必须在近场和远场中沿光轴上的不同位置进行五次的光束半径测量。⁴ 在不包含任何 TEM₀₀ 模式的情况下，可以使光束在一个特定平面上看起来像是理想高斯光束（图 2）。即使在特定平面上的横截面看起来像一个完美的高斯分布，光束的传播方式也会与高斯光束大相径庭，并且发散角更大。⁵ 在不同的平面上多次测量半径，可以很快看出这种光束与真正的高斯光束的区别。测量光束半径 (w(z))可以与束腰 (w₀)、波长 (λ) 和 M² 因子有如下关联 ⁶:

(4)$$ w \! \left( z \right) ^2 = w^2 _0 \left[ 1 + \left(z - z_0 \right)^2 \left( \frac{M^2 \lambda}{\pi w_0 ^2} \right)^2 \right] $$

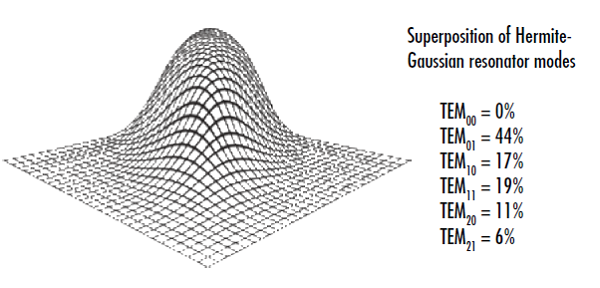
图 2: 该光束横截面在特定平面上呈高斯分布，即使不包含任何TEM00 模式也不例外，这说明沿激光轴进行多次强度测量以确定激光的 M<sup>2</sup> 因子的重要性

图 2: 该光束横截面在特定平面上呈高斯分布，即使不包含任何TEM₀₀ 模式也不例外，这说明沿激光轴进行多次强度测量以确定激光的 M² 因子的重要性

光束参数乘积

光束参数乘积 (BPP) 是评价光束质量的另一种度量，它被定义为束腰处光束半径与半角光束发散度的乘积。它通常用 mm mrad 表示，与 M²因子相关：

(5)$$ \text{BPP} = \frac{M^2 \lambda}{\pi} $$

由于 BPP 与 M² 因子成正比，因此光束参数乘积越大，光束的质量越差。BPP 的最小值是 λ/π，只有理想高斯光束才能获得此值。

桶中功率

桶中功率 (PIB) 是定义光束质量的另一种度量，通常用于大功率激光系统和材料加工应用。PIB 描述在指定“桶”（通常是被加工材料表面一个特定半径的点）上集成了多少激光功率。虽然这是一个看似简单的概念，但远场的桶形必须准确定义，与理想场景的比较取决于理想近场激光束形状的规格。
尽管没有行业标准的 PIB 确切定义，但它通常被称为垂直或水平光束质量: ⁷

(6)$$ \text{Vertical Beam Quality} = \sqrt{\frac{\text{Ideal Power in Bucket}}{\text{Actual Power in Same Bucket}}} $$

(7)$$ \text{Horizontal Beam Quality} = \frac{\text{Actual Beam Radius at a Given Power}}{\text{Ideal Beam Radius at the Same Power}} $$

与 M² 因子和 BPP 类似，PIB 值越低，光束质量越高。可以根据λ/D（D 是近场光束的直径）为所定义“桶”内的功率分数绘图，从而直观显示 PIB（图 3）。垂直光束质量是理想高斯光束的桶内功率分数与给定 λ/D 下真实光束的桶内功率分数（对应于图形中的垂直维度）之比的平方根。同样地，水平光束质量是理想高斯光束的 λ/D值与真实光束在桶内给定功率分数下的λ/D 值（对应于图形中的水平维度）的比率。

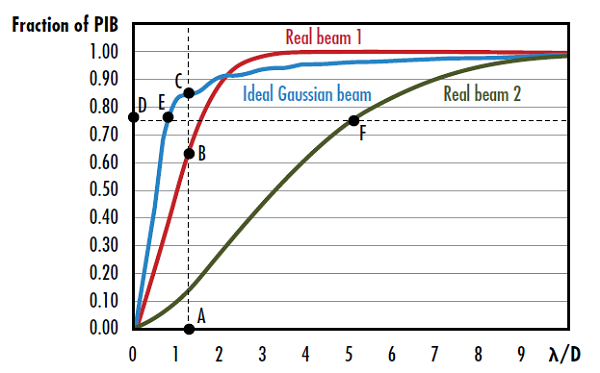
图 3: 真实光束 1 的垂直光束质量由 AC 段与 AB 段之比的平方根给出，真实光束 2 的水平光束质量由 DF 段与 DE 段之比给出7

图 3: 真实光束 1 的垂直光束质量由 AC 段与 AB 段之比的平方根给出，真实光束 2 的水平光束质量由 DF 段与 DE 段之比给出⁷

圆形与椭圆形光束

在考虑激光束形状时，确定激光器产生的光束是圆形还是椭圆形非常重要。由于半导体激光器的有源区域是矩形的，因此半导体激光器二极管会在 x、y 方向发射出发散角不同的椭圆形光束（图 4）。小光圈的衍射较大，由于有源区尺寸较小，因此会产生发散角更大的光束，并导致散光光束。发散角较大的轴定义为快轴，发散角较小的轴定义为慢轴。与圆形光束相比，椭圆形光束的聚焦点更大，这可能会对系统性能造成不利影响。更大的聚焦点会导致比圆形光束更低的辐照度（单位面积的辐射能通量），这就需要更高功率的激光。柱面透镜常被用来把椭圆光束整圆（图 5）。有关柱面透镜的更多信息，请参阅 “柱面透镜使用注意事项”。

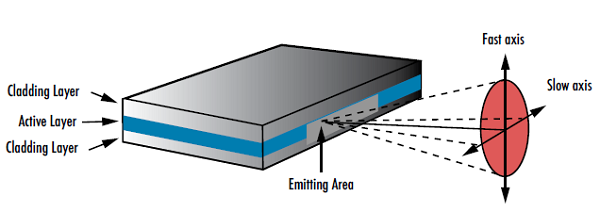
图 4: 激光二极管的几何形状导致它们产生具有两个不同发散角的椭圆形光束

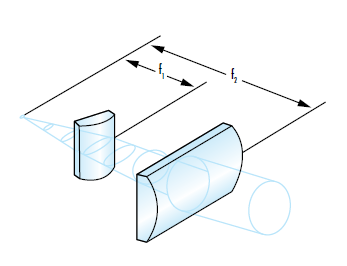
图 5: 通常将柱面透镜分别用于快轴和慢轴来使椭圆形光束变为圆形光束

斯特列尔比

正如 M² 因子将激光器的实际性能与理想光束进行比较一样，光学系统或组件的斯特列尔比也会将其实际性能与理想光束进行比较。聚焦光学元件（包括球面和非球面透镜）的斯特列尔比是某个点光源的实际光学元件的最大焦点辐照度与理论衍射极限光学的理想最大辐照度的比值（图 6）。⁷ 斯特列尔比为 1 表示光学元件完美，无畸变。行业规范通常认为透镜在斯特列尔比大于 0.8 时达到“衍射极限”。

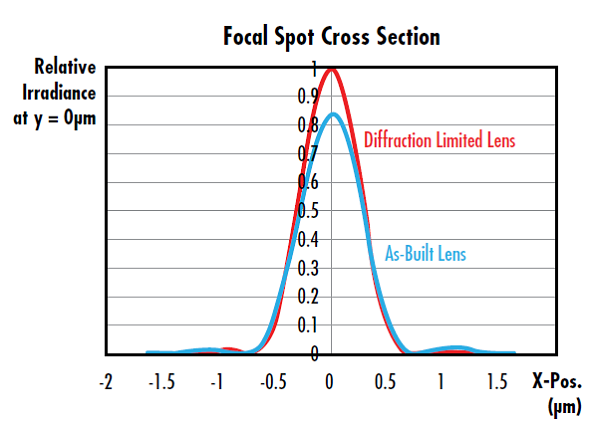
图 6: 该透镜的斯特列尔比为 0.826，由于大于 0.8，因此被认为是衍射极限

光学元件的斯特列尔比与等式 8 计算得出的 RMS 透射波前误差近似相关，其中 S 是光学元件的斯特列尔比，σ 是光学元件的 RMS 透射波前误差（以波为单位）。⁸ 当波前误差小于0.1个波时，这种近似是有效的。

(8)$$ S = \exp{\left[ - \left( 2 \pi \sigma \right)^2 \right]} $$

有关光学表面不规则性如何影响其斯特列尔比的信息，请参阅非球面透镜不规则性和斯特列尔比。

参考文献

International Organization for Standardization. (2005). Lasers and laser-related equipment – Test methods for laser beam widths, divergence angles and beam propagation ratios (ISO 11146).
A. E. Siegman, “New developments in laser resonators”, Proc. SPIE 1224, 2 (1990)
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
International Organization for Standardization. (2005). Lasers and laser-related equipment — Test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams (ISO 11146-1:2005).
A. Siegman, “’Non-Gaussian’ Beam”, OSA Annual Meeting, Long Beach, CA (1997)
Hofer, Lucas. “M² Measurement.” DataRay Inc., 12 Apr. 2016, www.dataray.com/blog-m2-measurement.html.
Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.