超快激光 — 超快相干性的基本原理
原子的概念是由二十四个世纪前的古希腊哲学家 Leucippus 和 Democritus 提出的。1 然而,直到 20 世纪后期,才可以观察到原子的运动并予以操控。2 原子尺度动力学的典型速度为 10km/s 数量级,运动距离为 1Å,对其进行操控所需的时间分辨率为 10 飞秒 (10×10-15 s)。 因此,若要实现原子和分子的可视化和操控,激光脉冲的持续时间需要达到原子核运动的数量级。激光技术的飞速发展使产生介于数飞秒到数十阿秒 (10×10-18 s)之间的脉冲成为可能。此类脉冲可实现对原子和电子的直接研究与操控,并将科技的前沿扩展到从未想到的领域。
激光器的运作基于两项一般原理:使用增益介质(例如 Ti:sapphire 晶体)对光进行放大,以及使用腔体(例如两面反射镜)确保反馈。在受激增益介质中对光进行放大时,由于腔体存在反馈(部分透射),因此会产生强烈的激光束(图 1)。
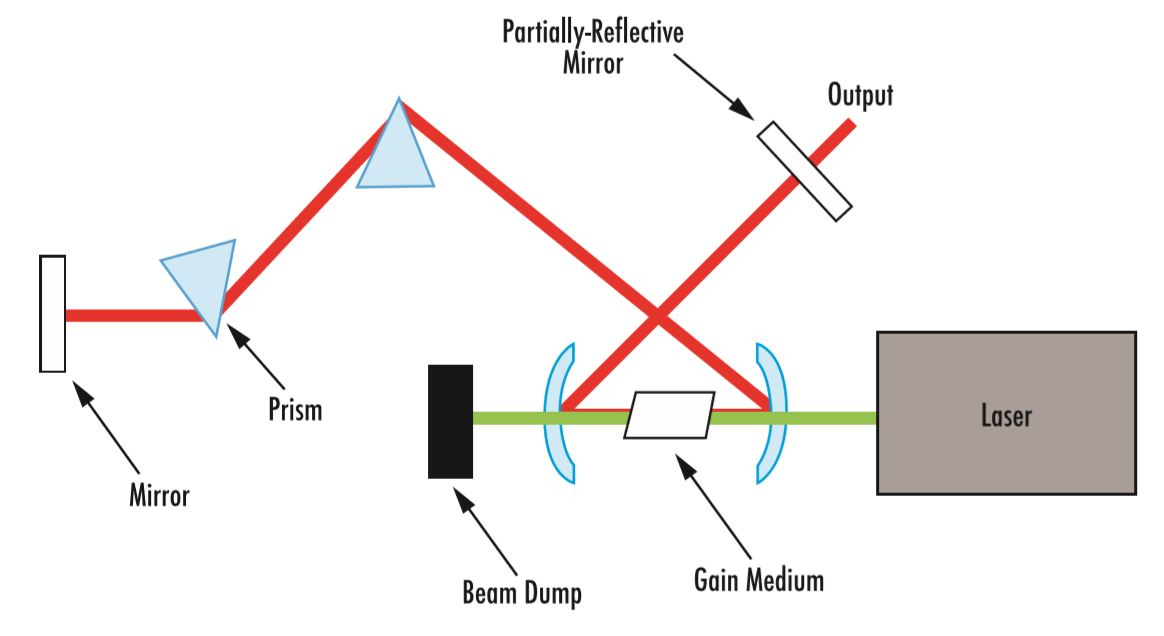
图 1: 使用连续波 (CW)、二次谐波生成、Nd:YAG 激光器的超快激光振荡器的典型光学设置
若光波具有大量的模或波长(λ)一半的整数倍,则光通过同相叠加以相干的形式发出(也称为锁模)时,会产生超短脉冲。超短脉冲的高能带宽是由光子固有波特性的不确定性原理决定的,其中时间能量的精度受傅里叶变换的限制。由于超短脉冲的能量(E=hc/λ) 可以跨越带宽的多倍频程,因此关键问题在于此类宽脉冲是否保持相干性。在超快尺度的光与物质的相互作用中,相干的概念对于确保光波与原子/电子群之间存在干涉效应极为重要。此类干涉的效果可能是相互增强,也可能是相互削弱,具体取决于两者之间的相位差(图 2)。3
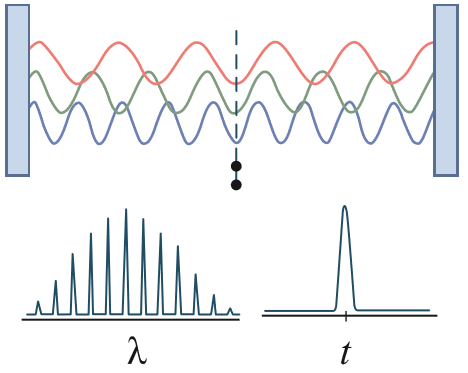
图 2:通过锁模产生超短脉冲(产生波长带宽很宽但时间宽度超短的脉冲)的基本概念
考虑高斯超快激光脉冲将系统从能量为E'0 的一种状态χ0 转换为能量为En的另一种状态φn , 波函数如下:
其中 αn是本征态 φn 的振幅,其模平方代表施加脉冲后各个本征态的总体概率。根据一阶微扰理论,可将这些本征态确定如下:
其中 C 是常数,取决于脉冲的场振幅和跃迁偶极矩, α = 2π2 / ln(2)。 < φn | χ0 > 是弗兰克-康登因子,由初始状态和最终状态之间的积分指定。对对公式 2 中的积分求值,结果如下 :
其中 ωn = (En - E'0) / ℏ 是玻尔频率。在超短脉冲的极限内, 激光激发过程的寿命(τ) 接近零, αn = C < φn | χ0 >. 因此, ψ = C <φn | χ0 > φn = χ0. 所以, 与初始波函数形状相同的受激波包络 ψ 是受激本征态的“相干” 叠加.
基于此形式,超快脉冲的相干特性为控制多级原子5、 分子6、 半导体自旋态7、相变89提供了强大的技术,从而实现了其他技术以前无法实现的应用。 使用超快激光,可以更好地理解新型材料中的结构功能范式,从而通过对原子、分子和单分子层的动态操控来设计功能优化的材料。10、11 以超精密测量技术和功能强大的材料为基础,对原子和电子动力学的准确探测和控制能力已带来一系列新颖的技术进步。
参考文献:
- B. Pullman, (1998). The Atom in the History of Human Thought. Oxford, England: Oxford University Press.
- H. C. von Baeyer, Taming the Atom; Random House: New York, 1992.
- A. H. Zewail, J. M. Thomas, 4D Electron Microscopy. Imaging in Space and Time; Imperial College Press, 2010.
- T. E. Karam, Ultrafast and Nonlinear Spectroscopy of Colloidal Nanomaterials. (2016).
- M.C. Stowe, A. Pe’er, J. Ye, Phys. Rev. Lett. 100, 203001 (2008).
- M. Viteau, A. Chotia, M. Allegrini, N. Bouloufa, O. Dulieu, D. Comparat, P. Pillet, Sci. Agric. 321, 232 (2008).
- D. Press, K.D. Greve, P.L. McMahon, T.D. Ladd, B. Friess, C. Schneider, M. Kamp, S. Höfling, A. Forchel, Y. Yamamoto, Nat. Photonics. 4, 367 (2010).
- J. Hu, G. M. Vanacore, Z. Yang, X. Miao, A. H. Zewail. ACS Nano 9, 6728 (2015).
- Kimel, A. V., A. Kirilyuk, P. A. Usachev, R. V. Pisarev, A. M. Balbashov, Th. Rasing. Nature 435, 7042 (2005).
- Hu, J., Karam, T.E., Blake, G.A. and Zewail, A.H., Chem. Phys. Lett. 683, 258 (2017).
- Kaplan, M., Yoo, B.K., Tang, J., Karam, T.E., Liao, B., Majumdar, D., Baltimore, D., Jensen, G.J. and Zewail, A.H. Angew. Chem. Int. Ed. 56, 11498 (2017).










































或查看各区域电话
报价工具
只需输入商品编号
Copyright 2023, 爱特蒙特光学(深圳)有限公司。— 广东省深圳市龙华工业东路利金城科技工业园3栋5楼 518109 - 粤ICP备2021068591号