超快激光的激光损伤阈值
This is Section 3.6 of the Laser Optics Resource Guide.
超快激光是锁定模式的脉冲激光,能发出持续时间级短且峰值功率很高的脉冲。由于傅里叶极限(或称为能量-时间不确定性),较短的时间脉冲长度对应较宽的波长谱传播,因此与较长的脉冲相比,超快脉冲具有更宽的波长带宽(图 1)。超快激光器广泛应用于包括高强度物理、飞秒材料处理和激光光谱学在内的各种领域。1
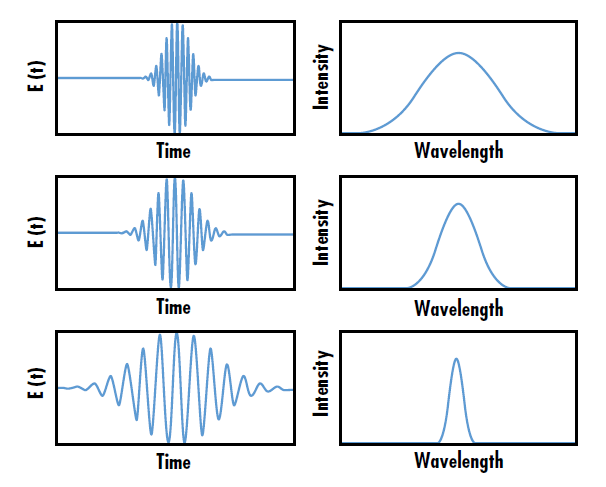
图 1: The wavelength bandwidth of ultrafast laser pulses is inversely related to the pulse duration
近年来,超快激光诱导损伤已成为一个活跃的研究课题,因为超快激光极短的脉冲持续时间会导致其与光学镀膜和组件发生不同于其他脉冲激光器的相互作用。一般来说,超快激光照射后薄膜镀层的升温是由非平衡能量透射引起的。入射光子的能量被基态电子吸收,从而在几飞秒内占据激发态。然后,这些“热”电子通过皮秒级的声电子和声子-声子散射重新回到基态,使镀膜材料能够重新进行能量分布。2, 3 声电子散射描述了晶格振动引起的电子波函数的畸变,声子-声子散射描述了晶格振动引起晶格内其他振动 (图 2)。

图 2: 声子-电子散射是晶格振动和电子之间的能量传递,重定向晶格内的电子。另一方面,声子-声子散射是多个晶格振动相互作用以产生新声子的过程
由于电子的费米分布比电子晶格重新分布快得多,因此薄膜可以描述为电子和声子这两个子系统相互作用的合成物。4 了解超快激发引起的温升对理解超快激光器的 LIDT 至关重要。热载子驰豫动力学可以用超快泵浦-探测光谱技术进行理论计算和实验验证,该光谱技术可以测量测试光学性质随时间的变化。5, 6
超快激光器激发下的电子和晶格热行为可以用两个温度模型描述,它们假设电子和晶格子系统独立、自发达到平衡。采用耦合热容方程确定超快激发时的理论温升,公式为:7
- Ce 和 Cl 是电子和晶格子系统的热容
- Te 和 Tl 是电子和晶格的温度
- ke 是电子的导热系数
- S 是超快激光脉冲根据时间 (t) 和空间 (z) 采用的加热期
- G 为电子晶格耦合常数,计算公式为:
- me 是有效电子质量
- ne 是电子数密度
- cs 是大块材料的声速,描述为体积模量 B 与密度 ρm 之比的平方根
- τ(Te) 是电子弛豫时间
等式 1、等式 2 和等式 3 用于提供时间函数 Tl 和 Te。图 3 显示为聚焦在 800 nm 处,并通过直径为 120μm 的光束照亮悬浮在铜基片上的 200nm 厚金纳米膜的 0.2 J/cm2 10fs 超快激光脉冲计算得出的理论 Tl 和 Te。金纳米膜的厚度远远大于光学元件和电子对纳米膜的穿透深度。
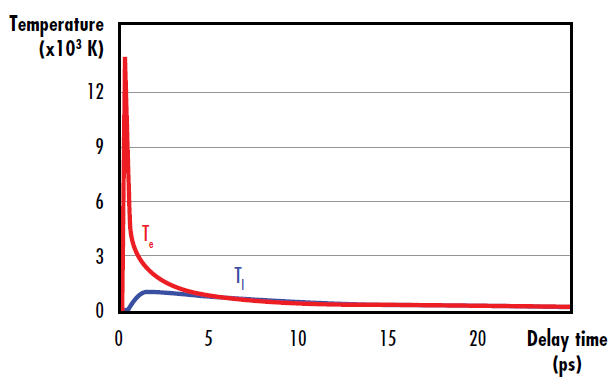
图 3: 当 0.2 J/cm2 10fs 超快激光脉冲聚焦在 800nm 处时,随时间变化的电子(红色)和晶格(蓝色)将升温。金纳米薄膜由于晶格温度升高而升温,并导致激光诱导损伤萌发
The electron temperature quickly reaches extremely high temperatures (13,000K). Electron-lattice equilibration processes then lead to an increase in the lattice temperature (Tl), which reaches values of around 1,300K. Tl is on the same order of the melting temperature of gold (1,337K); this relatively weak ultrafast pulse with a fluence of only 0.2 J/cm2 caused the lattice to reach the melting point of gold.
非平衡系统通过电子-声子散射和声子-声子散射来耗散能量,从金纳米膜到周围铜基片的延迟能量转移提供了额外的能量耗散通道。晶格温度的升高会导致镀膜中出现激光诱导损伤。了解超快激光激发后的超快再热对设计和优化适用于超快激光应用的光学镀膜至关重要。
超快脉冲的理论影响可以通过超快泵浦-探测光谱技术(如超快电子衍射)实验验证。超快泵浦光束用于激发试样,低功率探针光束则用于监测非平衡态引起的电子衍射强度变化(图 4)。电子衍射强度的变化与泵浦和探测光束中的脉冲到达时间之间的延迟相关,揭示了电子-晶格的动态变化。8 这样的动力变化显示了激发电子的弛豫路径,从而导致纳米膜升温。
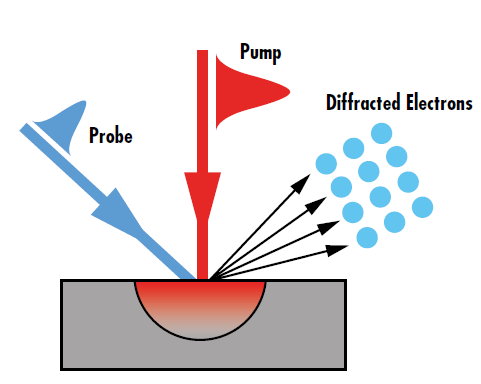
图 4: 通过泵浦-探测光谱技术观察到的衍射强度变化直接关系到超快激光激发引起的非平衡能量传输
超快激光器引起的衍射强度变化受 Debye-Waller 效应控制,计算公式为:
- I(t) 是 t 时刻的衍射强度
- I0 是初始强度
- T0 是初始温度
- u2 (T)为原子均方位移,计算公式为:
- ħ i是降低的普朗克常数,或普朗克常数除以 2π
- m 是单位细胞的有效质量
- kB 是玻尔兹曼常数
- θD 是德拜温度
等式 4 和等式 5 显示在激光不同泵浦-探测时间延迟下激发后的衍射强度变化。探测和泵浦光束照亮的是光学元件表面还是镀膜-基片界面也会导致衍射强度变化不同(图 5)。超快激发后系统达到平衡温度的延迟时间要比超快脉冲持续时间长得多。纳米薄膜的升温就在几微秒内,由超快激光激发后受激电子的平衡引起。

图 5: 在金纳米膜超快激发后的电子-声子和声子-声子散射的衍射强度变化(蓝色)以及从金纳米膜到铜基片的能量转移导致的金-铜界面衍射强度变化(红色)
参考文献
- Mao, S. S. et al., “Dynamics of Femtosecond Laser Interactions with Dielectrics.” Appl. Phys. A 2004, 79, 1695.
- Jiang, L., and H. l. Tsai. “Energy Transport and Material Removal in Wide Bandgap Materials by a Femtosecond Laser Pulse.” International Journal of Heat and Mass Transfer, vol. 48, no. 3-4, 2005, pp. 487–499., doi:10.1016/j.ijheatmasstransfer.2004.09.016.
- Wellershoff, Sebastian S., et al. “The Role of Electron–Phonon Coupling in Femtosecond Laser Damage of Metals.” Appl. Phys. A, vol. 69, Dec. 1999, pp. 99–107.
- Shin, Taeho, et al. “Extended Two-Temperature Model for Ultrafast Thermal Response of Band Gap Materials upon Impulsive Optical Excitation.” The Journal of Chemical Physics, vol. 143, no. 19, 2015.
- Karam, Tony E, et al. “Enhanced Photothermal Effects and Excited-State Dynamics of Plasmonic Size-Controlled Gold–Silver–Gold Core–Shell–Shell Nanoparticles.” J. Phys. Chem, vol. 119, 17 July 2015, pp. 18573–18580., doi: 10.1021/acs.jpcc.5b05110.
- Heilpern, Tal, et al. “Determination of Hot Carrier Energy Distributions from Inversion of Ultrafast Pump-Probe Reflectivity Measurements.” Nature Communications, vol. 9, no. 1, Oct. 2018, doi:10.1038/s41467-018-04289-3.
- Hu, Jianbo, et al. “Ultrafast Lattice Dynamics of Single Crystal and Polycrystalline Gold Nanofilms☆.” Chemical Physics Letters, vol. 683, 2017, pp. 258–261., doi:10.1016/j.cplett.2017.04.021.
- Gedik, Nuh. “Techniques.” Gedik Group, Massachusetts Institute of Technology, 2013, web.mit.edu/gediklab/research.html













 上个章节
上个章节 





























或查看各区域电话
报价工具
只需输入商品编号
Copyright 2023, 爱特蒙特光学(深圳)有限公司。— 广东省深圳市龙华工业东路利金城科技工业园3栋5楼 518109 - 粤ICP备2021068591号